Are there any computational origami people on here?
-
Are there any computational origami people on here? I keep thinking about the #foldology puzzles and started to write a python class to describe the puzzles (how hard could it be it’s on a fixed grid, right? oh no no no) I think I’ve run into one of those big “hard” problems in a naive way:
Q. Is it possible to represent every origami fold as a sequence of 2D creases on a flat surface (no not even close?)
This has lead me to the phrase “computational origami” are there any popular books?

-
Are there any computational origami people on here? I keep thinking about the #foldology puzzles and started to write a python class to describe the puzzles (how hard could it be it’s on a fixed grid, right? oh no no no) I think I’ve run into one of those big “hard” problems in a naive way:
Q. Is it possible to represent every origami fold as a sequence of 2D creases on a flat surface (no not even close?)
This has lead me to the phrase “computational origami” are there any popular books?

@futurebird I'm not but you've got me to search for it and now I'm fascinated

-
Are there any computational origami people on here? I keep thinking about the #foldology puzzles and started to write a python class to describe the puzzles (how hard could it be it’s on a fixed grid, right? oh no no no) I think I’ve run into one of those big “hard” problems in a naive way:
Q. Is it possible to represent every origami fold as a sequence of 2D creases on a flat surface (no not even close?)
This has lead me to the phrase “computational origami” are there any popular books?

@futurebird Origami is Turing complete, so this rabbit hole runs deep. I enjoyed Quanta’s articles on this https://www.quantamagazine.org/tag/origami/
-
Are there any computational origami people on here? I keep thinking about the #foldology puzzles and started to write a python class to describe the puzzles (how hard could it be it’s on a fixed grid, right? oh no no no) I think I’ve run into one of those big “hard” problems in a naive way:
Q. Is it possible to represent every origami fold as a sequence of 2D creases on a flat surface (no not even close?)
This has lead me to the phrase “computational origami” are there any popular books?

@futurebird I looked into this maybe 15-20 years or so ago, after being enraptured with Modular Origami. I had stacks of books on the subject. Tomoko Fuse FTW!
At the time, there were a few research papers on the subject of computational origami, but I found them very unapproachable.
I did the same thing you did, and ended up writing my own DSL for describing sequences of folds. (This was in XML, for a sense of the time.) It basically boiled down to "starting with flat paper of this size and shape, here are the series of polygon cuts and rotations to get to the final 3D shape". I never got farther than that. I tried to do some OpenGL visualization (with SDL) and got so frustrated with it that I gave up the entire project.
But in the intervening years, I know NASA and other space agencies have thrown a ton of money at this. Space packing, self-expanding structures, that sort of thing.
Sorry I can't give you any solid links. I'm curious to see what you'll find these days!
-
Are there any computational origami people on here? I keep thinking about the #foldology puzzles and started to write a python class to describe the puzzles (how hard could it be it’s on a fixed grid, right? oh no no no) I think I’ve run into one of those big “hard” problems in a naive way:
Q. Is it possible to represent every origami fold as a sequence of 2D creases on a flat surface (no not even close?)
This has lead me to the phrase “computational origami” are there any popular books?

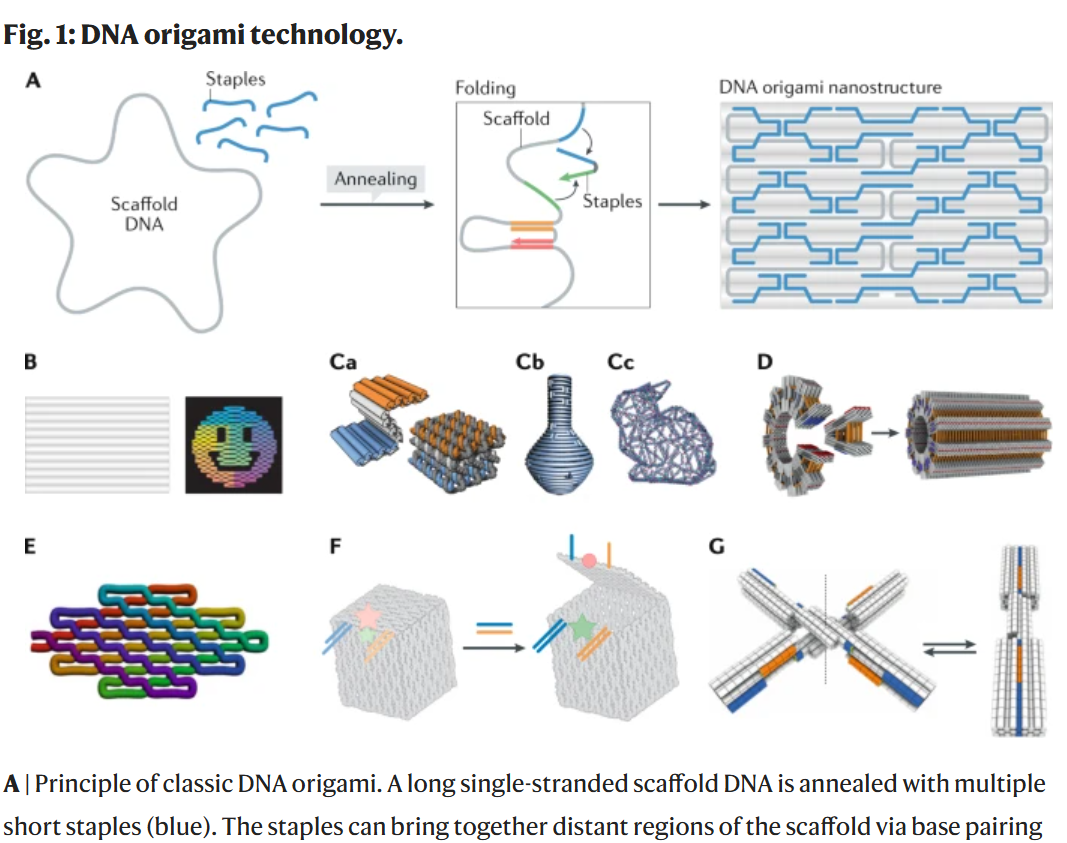
Peripherally related, you can make DNA fold into little shapes, this is called DNA origami, and there are lots of computational tools to design shapes.
https://www.nature.com/articles/s43586-020-00009-8
-
Peripherally related, you can make DNA fold into little shapes, this is called DNA origami, and there are lots of computational tools to design shapes.
https://www.nature.com/articles/s43586-020-00009-8

@MCDuncanLab Don't let the plutocrats get wind of this or we'll have another bubble when the "AI" one bursts. "DNA stapples for therapeutics" and some such shit. @futurebird
-
Are there any computational origami people on here? I keep thinking about the #foldology puzzles and started to write a python class to describe the puzzles (how hard could it be it’s on a fixed grid, right? oh no no no) I think I’ve run into one of those big “hard” problems in a naive way:
Q. Is it possible to represent every origami fold as a sequence of 2D creases on a flat surface (no not even close?)
This has lead me to the phrase “computational origami” are there any popular books?

@futurebird Robert Lang has done extensive research about the math of origami. His book Origami Design Secrets would be where I would look. Or you can contact him directly I guess.
-
Are there any computational origami people on here? I keep thinking about the #foldology puzzles and started to write a python class to describe the puzzles (how hard could it be it’s on a fixed grid, right? oh no no no) I think I’ve run into one of those big “hard” problems in a naive way:
Q. Is it possible to represent every origami fold as a sequence of 2D creases on a flat surface (no not even close?)
This has lead me to the phrase “computational origami” are there any popular books?

@futurebird My wife loves origami and recommends this book by Robert J Lang (she hasn't read it (yet) but it's apparently huge in the origami world): https://langorigami.com/publication/origami-design-secrets-2nd-edition/
He's also done a TED talk and made a Google Doodle: https://langorigami.com/article/doodling-with-sensei/
-
Are there any computational origami people on here? I keep thinking about the #foldology puzzles and started to write a python class to describe the puzzles (how hard could it be it’s on a fixed grid, right? oh no no no) I think I’ve run into one of those big “hard” problems in a naive way:
Q. Is it possible to represent every origami fold as a sequence of 2D creases on a flat surface (no not even close?)
This has lead me to the phrase “computational origami” are there any popular books?

@futurebird @divbyzero writes about this.
-
Are there any computational origami people on here? I keep thinking about the #foldology puzzles and started to write a python class to describe the puzzles (how hard could it be it’s on a fixed grid, right? oh no no no) I think I’ve run into one of those big “hard” problems in a naive way:
Q. Is it possible to represent every origami fold as a sequence of 2D creases on a flat surface (no not even close?)
This has lead me to the phrase “computational origami” are there any popular books?

@futurebird Have a look through the JWST publications; I believe they surveyed the field when they were working out how to unfold their mirrors.
-
Are there any computational origami people on here? I keep thinking about the #foldology puzzles and started to write a python class to describe the puzzles (how hard could it be it’s on a fixed grid, right? oh no no no) I think I’ve run into one of those big “hard” problems in a naive way:
Q. Is it possible to represent every origami fold as a sequence of 2D creases on a flat surface (no not even close?)
This has lead me to the phrase “computational origami” are there any popular books?

-
R relay@relay.infosec.exchange shared this topic
